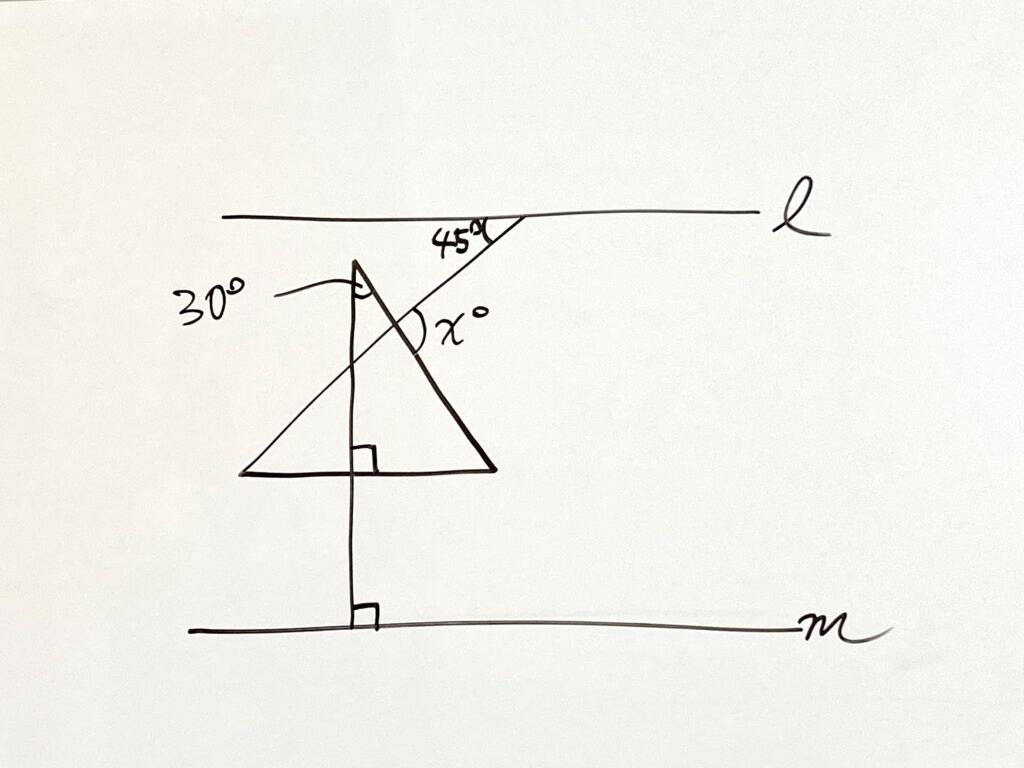
お年玉 〜錯角の拡張概念〜
新年明けましておめでとうございます。
ワクワク塾 塾長の福田歩です。
塾生たちにはクリスマスプレゼントとして紹介したのですが、
12月に『錯角の拡張概念』を思いつきました。
私立の早いところでは今週末あたりから入試が始まります。
お年玉がわりに
知ってると秒殺できる裏技を公開!!
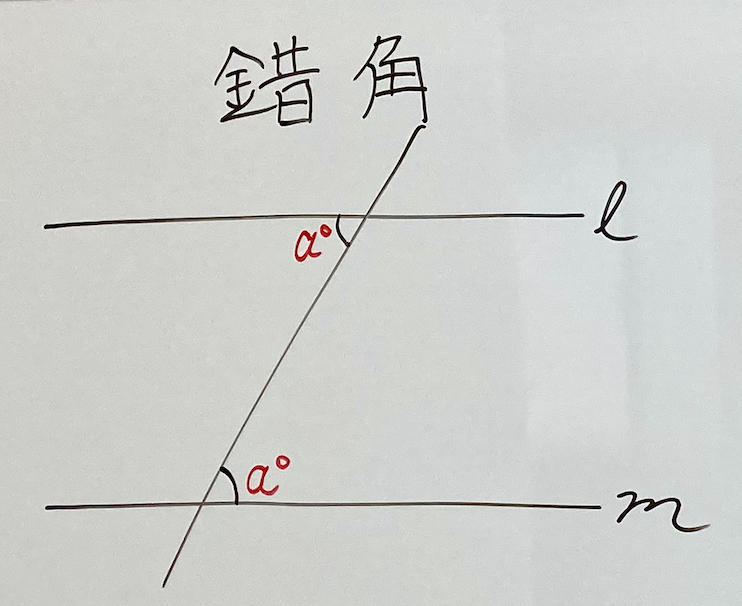
まず、基本の確認。
「錯角」「同位角」「対頂角」
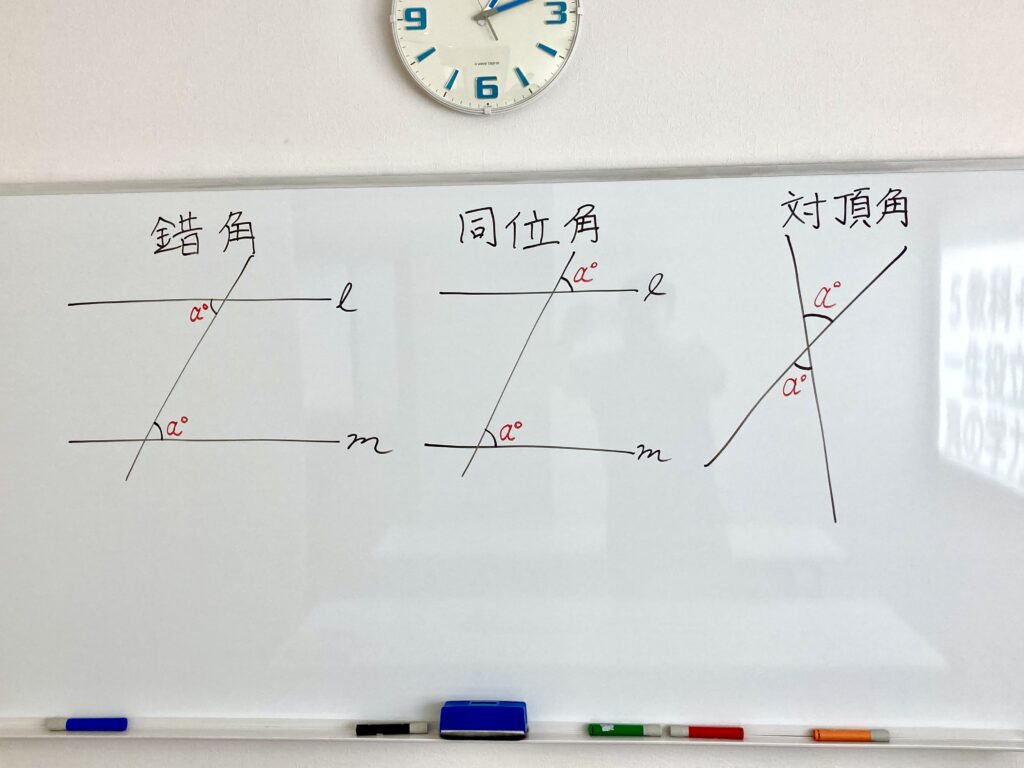
さて、『錯角』の “見え方” を変えていきます。
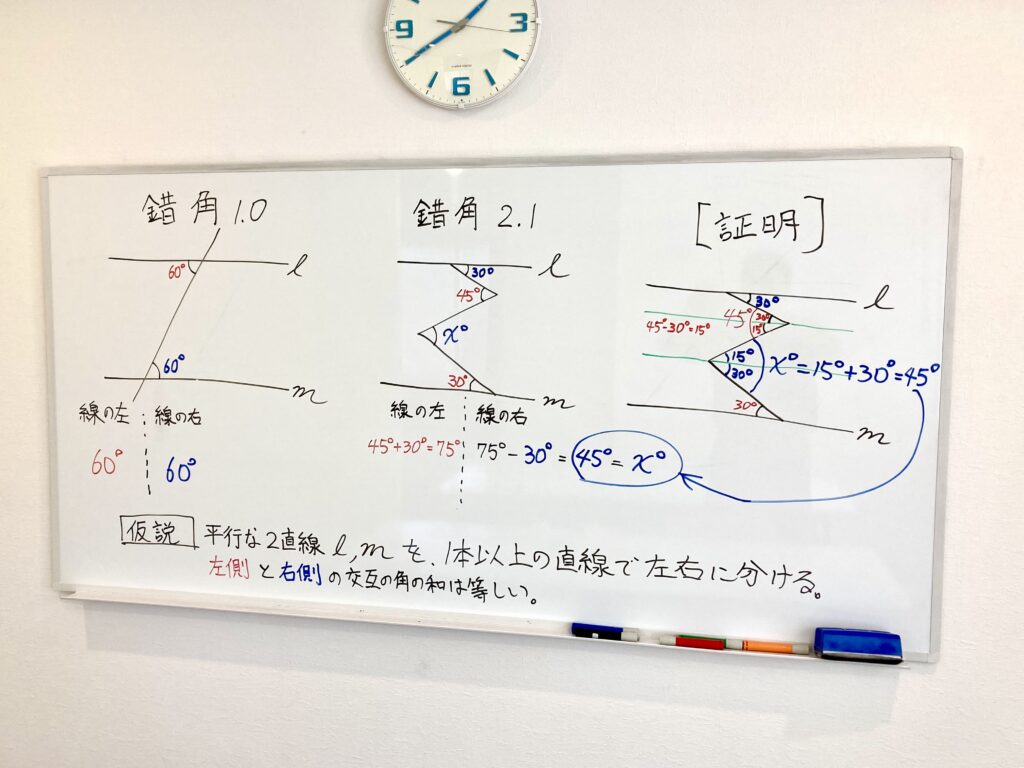
下の図のように、
“並行な2直線 l と m を
1本以上の直線で左右に分けるとき、
線の左側と右側に交互にできる角の和は等しい”
と仮定して、証明していきます。
『錯角』の概念で簡単に証明できますね。

左右に分ける線の数を増やしても成り立つ。
↓↓ 錯角 2.1
だったら、左右に分ける線は
下っていく線ばかりではなく、
上ったり下ったりしても良いんじゃない!?
↓↓ 錯角 3.0
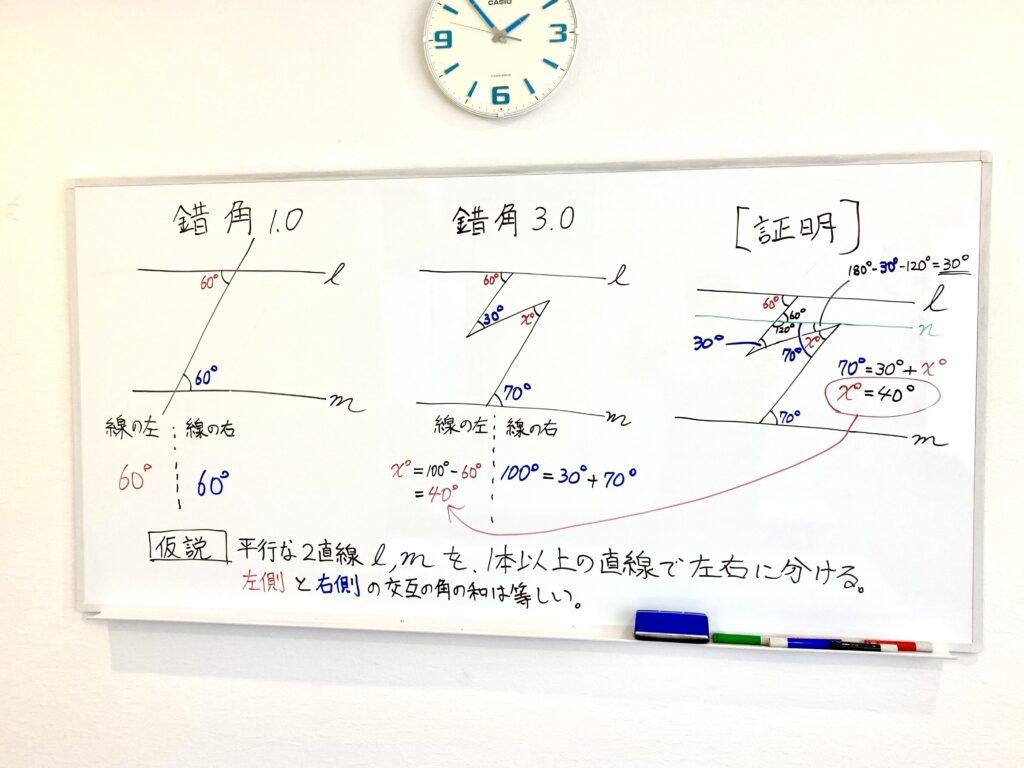
この証明が納得できたなら、
使っていいよね!!
数学に限らずだけど、
「新しい見え方」「新しいアイディア」に気づくと楽しいよね。
それを証明できたときの感動を味わってほしい!!
ちなみに、「錯角」は英語で “alternate angles”
直訳すると “交互の角” という意味だよ。
まさに1.0〜3.0の概念をわかっている人がつけた名前だろうね。
alternate(形容詞);交互の、かわるがわるの、一つおきの、互い違いの
基本として習う「錯角」も「交互の角」だけど、
拡張概念「互い違いの角の和」に気づかないと
もったいない気がするね。
ということで
こんな問題も、もう秒殺だよね!?